- 联系方式:1761430646@qq.com
- 菜狗摸索,有误勿喷,烦请联系
1. 赛马问题
-
问题
- 一共有 64 匹马和 8 条赛道,选出跑的最快的前 4 的马,需要至少比几场比赛?(一场比赛最多占 8 条赛道)
- 注意:这里是没有计时器之类的东西,只能单纯的通过比一场才知道谁跑的块,谁跑的慢。
- 马可能不会尽全力跑,但是跑的快的马 在比赛中一定会跑的 比跑的慢的马 快
-
思路
-
任意一匹马都可能是黑马,是可能可以跑进前 4 的,也即可能是目标马,不跑就不知道结果,所以每一匹马都要跑一趟先
-
64 匹马,8 条赛道,一次跑 8 匹,此时总共跑 8 场
-
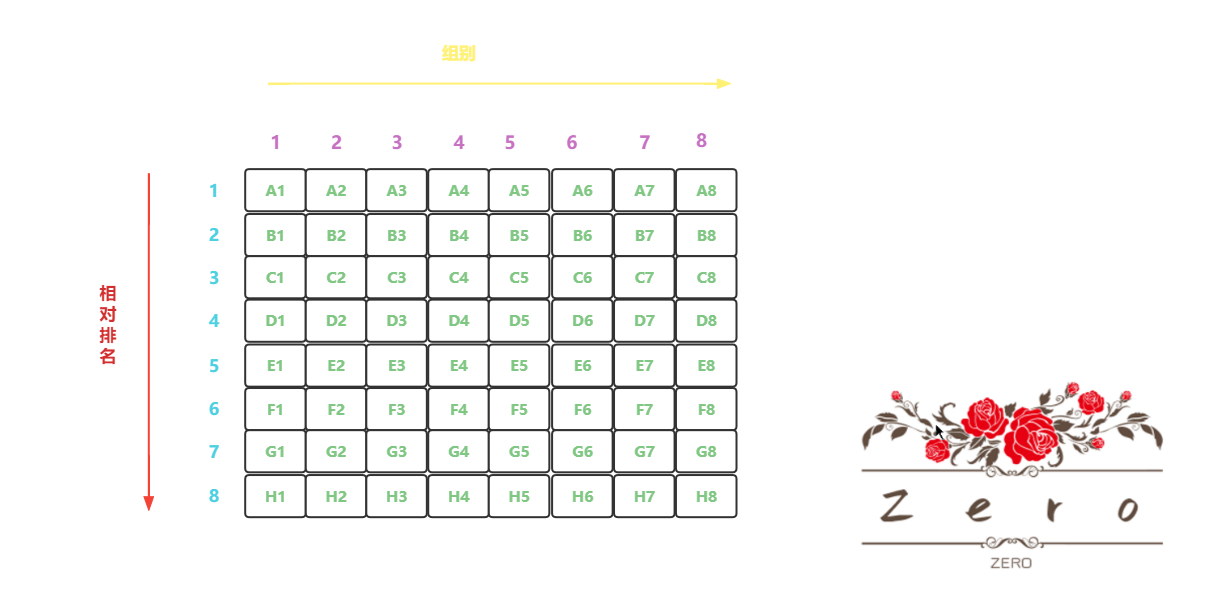
跑完后我们就可以得知这 8 组的马的排名了,假如排名可能如下图
-
我们想要跑的前 4 的马,这 4 匹马,可能分散在多个组中,也可能只落在一个组中
-
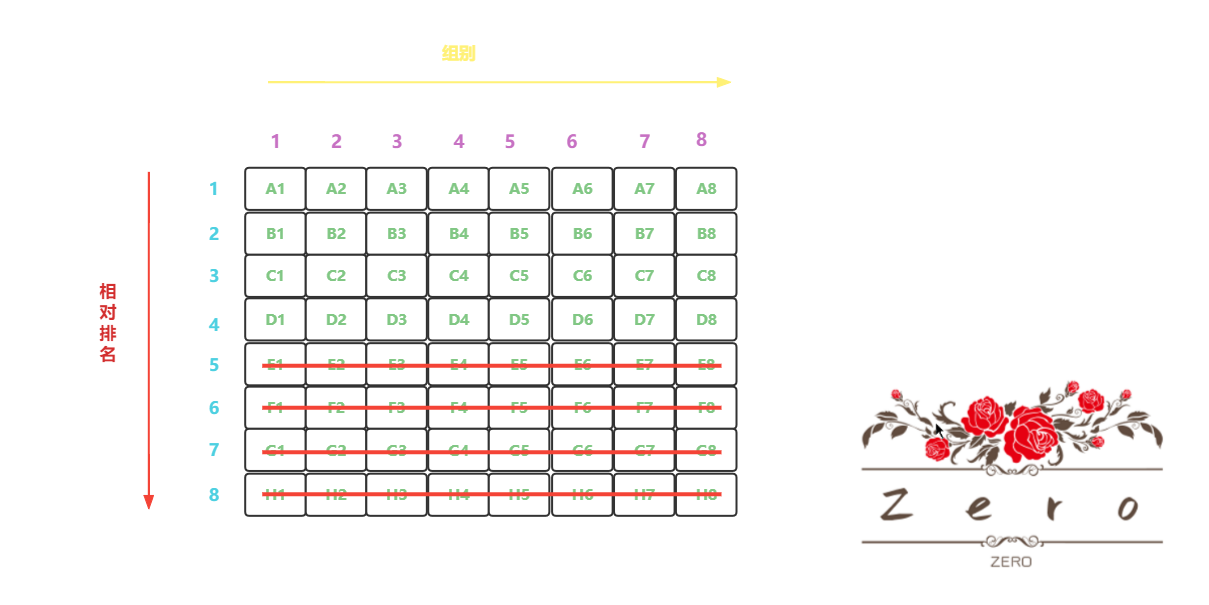
由于求至少比赛场数,也即需对最坏情况进行评估,而最坏情况,无非就是 4 匹马都同时落在了同一组中,我们只要前 4,那么这代表着对于每一组,后 4 名的马永远不可能是答案,所以经过分析后,我们可以排除 8 * 4 匹马
-
经过此次排除后,我们还是不能确定到底是哪 4 匹马是目标,所以,接下来我们需要让这 8 组的每个第一名拉出来组织比一场
- 为什么是选每个组内的第一名跑,个人感觉,如果说选每个组内第一名出来跑一场得到一个排名 X,那么至少,至少我们最直观的感觉是可以从这个排名 X 中可以得知 排名 X 中的第一名一定是所有马中跑的最快的那一匹(所在组内第一名,与其他组的第一名跑一场也是第一名),然后再往下推导。
- 但是如果是其他选择,比如说选每个组内的最后一名,或者是处在中间的马,得到新排名 Y 后会发现好像推不出什么来。
- 个人觉得对于这种不知道怎么选择的问题,一般性通用解决方案都是往每种可能都往下推导一遍。而题目是要求选最快的,我们可以在选择推导方案时时,偏向于选跑的最快的马出来跑一趟,推导方向不一定是对的,但至少有很大概率上可以帮助我们
-
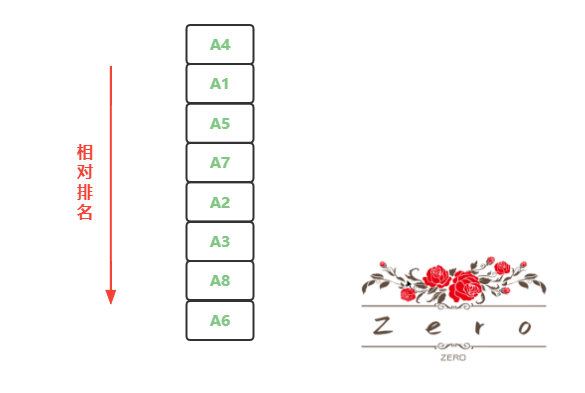
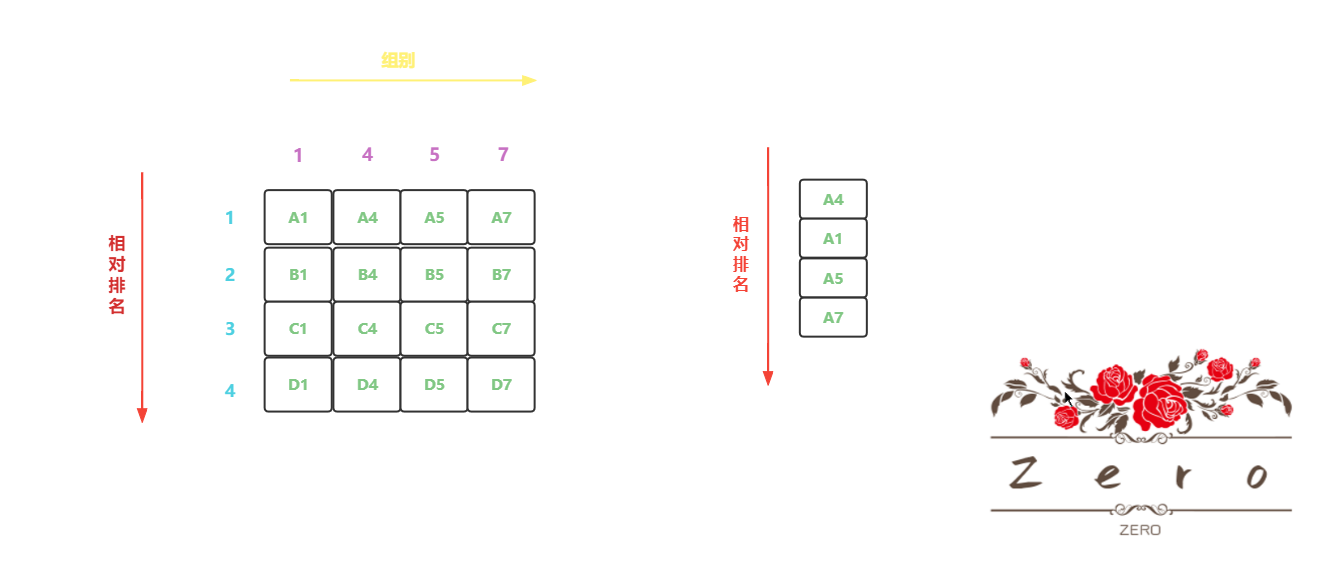
经过这次比赛,我们可能得到了如下排名情况
-
我们要求跑的最快的前 4 马,那么目标马一定会出现在这次排名中前面 4 位所在的组,也就是说这次排名的后4名马的所在组不可能目标马会出现在其中
- 后面 4 名的马分别是它们组内跑的最快的马,但是跟其他组的第一名跑连前 4 都跑不进,这也意味着跟它们同一组的其他马,原本跑的比它们组内第一名还慢,而它们组内第一名连前 4 跑不进,那么同组其他马更别想跑进前 4 了,所以可以排除了
-
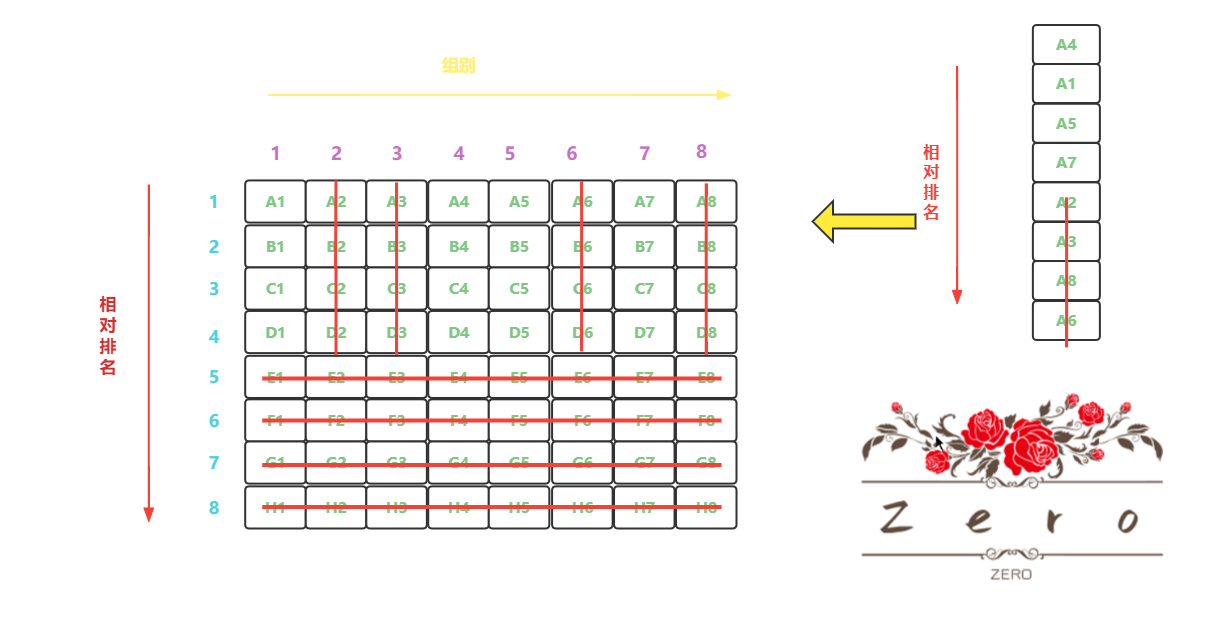
排除了 4组 * 4的马后,我们还剩下 4组 * 4 的马的情况
-
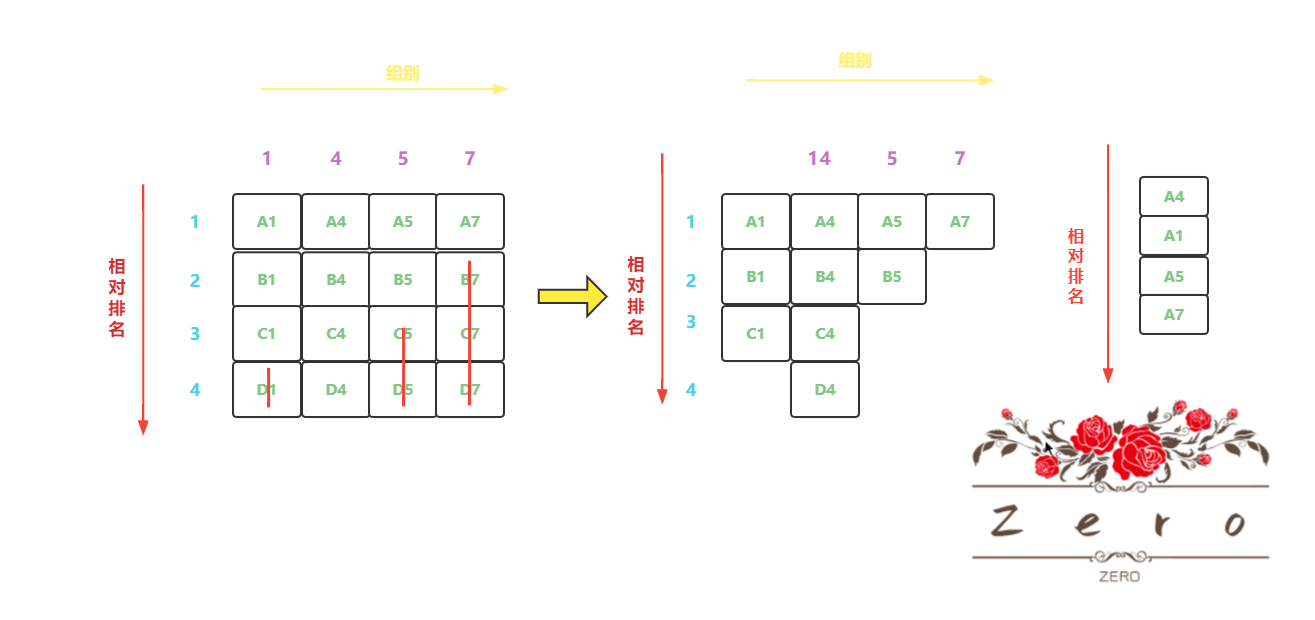
接下来继续分析,首先,上一次排名第 4 名的 A7 号马所在组第 7 组的最后 3 匹马( B7,C7,D7 )绝不可能是目标马,因为此时最乐观的情况无非也就是 A7 刚好是所有马中跑的最快的第 4 名
-
同理,可推上一次所得排名第 3 名的 A5 号马所在组第 5 组的最后 2 匹马( C5,D5 )绝不可能是目标马,可推上一次所得排名第 2名的 A1 号马所在组第 1 组的最后 1 匹马( D1 )绝不可能是目标马,此时,所剩下马的情况如下图
-
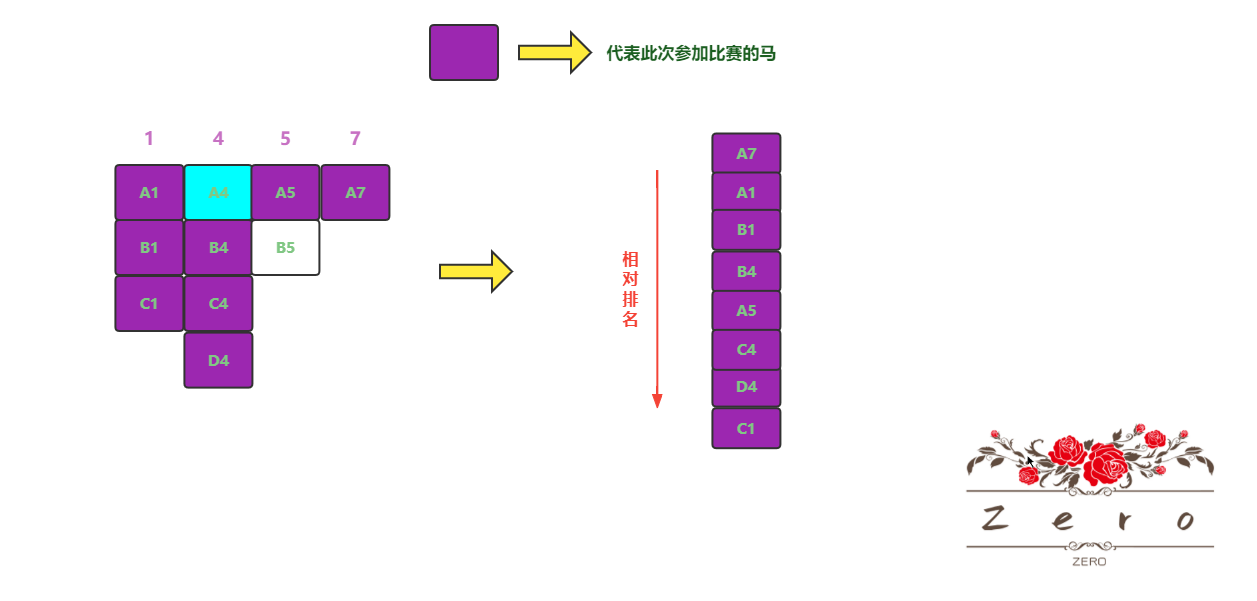
对于 A4 号马,它是第 4 组的第一名,也是每组第一名拉出来比赛的第一名,无可置疑,它就是所有马中跑的最快的那一匹,也即为目标马
-
剩下的 9 匹马,暂且还是不知道跨组间的马到底是谁跑的快,所以抽 8 匹马拉出来再比一躺(注意:这还有一匹不参加比赛的马,这匹马一定是它当前所在组的最后一名,这样根据此次比赛排名后,乐观情况下可以少比一次–最后面就会讲到),假设比赛结果如图所示
-
回顾问题,我们要求跑的最快的前 4 马,由上述可知, A4 号马是第一名,是目标马,还剩下选 3 匹,所以在这次排名中,后面 5 名的马决不可能是答案,排除掉,那么现在只剩下 这次排名前 3 的马(
A7,A1,B1)和 一匹这次没有参与到比赛的马B5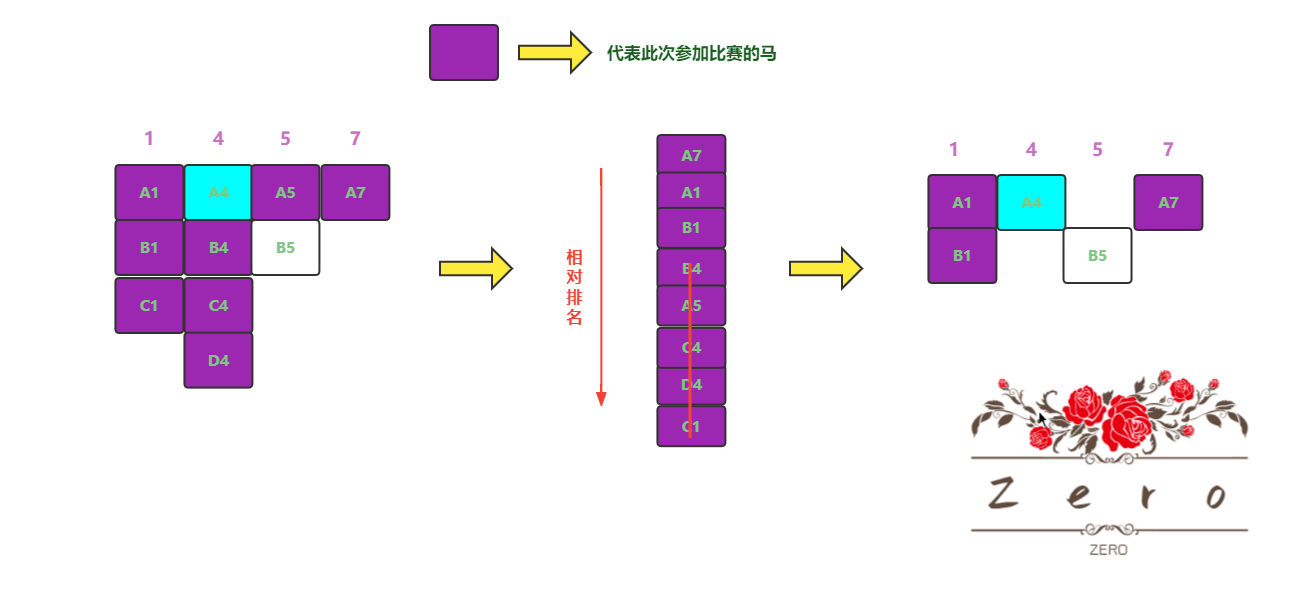
- 而
B5号马是可以通过A5号马的排名可以推出的,如果说A5号马在此次排名后5名,A5号马被淘汰,那么B5号马跑的比A5慢,B5号马也会被淘汰,所以绝不可能是目标马,此时总共比较 10 场 - 但是如果说
B5号马是此次排名的第 1 或者第 2 名,那么B5号马也很有可能是目标马,此时需要再比多一躺,那么此时总共比较 11 场 - 可以看出,对于这一匹不参与比赛的马,如果选的是每组中的最后一名,那么最后比较时乐观情况下是可以少赛一场的,但是如果不是每组中的最后一名,那么最后肯定还是要多赛一场的。所以,这也就是我们之前选一匹不参与比赛的马时,选的是其在所在组最后一名的原由了
- 而
-
所以,至少要比 11 场比赛才能选出前 4 的马
-


